Fraction of variance unexplained
In statistics, the fraction of variance unexplained (FVU) in the context of a regression task is the fraction of variance of the regressand Y which cannot be explained, i.e., which is not correctly predicted, by the explanatory variables X.
For a more general definition of explained/unexplained variation/randomness/variance, see the article explained variation.
Formal definition
Given a regression function ƒ yielding for each yi, 1 ≤ i ≤ N, an estimate 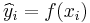 , we have:
, we have:
where R2 is the coefficient of determination, and SSerr (the sum of squared predictions errors, equivalently the residual sum of squares), SStot (the total sum of squares), and SSreg (the sum of squares of the regression, equivalently the explained sum of squares) are given by
Alternatively, the fraction of variance unexplained can be defined as:
where MSE(f) is the mean squared error of the regression function ƒ.
Explanation
It is useful to consider the second definition to get the idea behind FVU. When trying to predict Y, the most naïve regression function that we can think of is the constant function predicting the mean of Y, i.e., 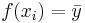 . It follows that the MSE of this function equals the variance of Y; that is, SSE = SST, and SSR = 0. In this case, no variation in Y can be accounted for, and the FVU then has its maximum value of 1.
. It follows that the MSE of this function equals the variance of Y; that is, SSE = SST, and SSR = 0. In this case, no variation in Y can be accounted for, and the FVU then has its maximum value of 1.
More generally, the FVU will be 1 if the explanatory variables X tell us nothing about Y in the sense that the predicted values of Y do not covary with Y. But as prediction gets better and the MSE can be reduced, the FVU goes down. In the case of perfect prediction where 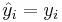 , the MSE is 0, SSE = 0, SSR = SST, and the FVU is 0.
, the MSE is 0, SSE = 0, SSR = SST, and the FVU is 0.
![\begin{align}
\text{FVU} & = {SS_{\rm err} \over SS_{\rm tot}} = 1-{SS_{\rm reg} \over SS_{\rm tot}} \\[6pt]
& = 1 - R^2,
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/4265c0d924e5f3a3ee679c66c5f1febd.png)
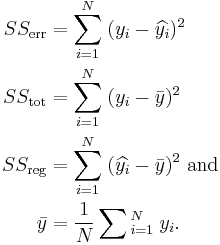
![\text{FVU} = \frac{\text{MSE}(f)}{\text{var}[Y]},](/2012-wikipedia_en_all_nopic_01_2012/I/392f4b49460ff167c7716889a015c24b.png)